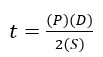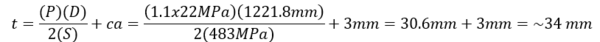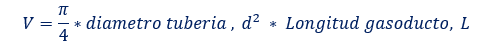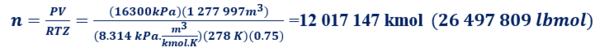Gasoducto de Larga Distancia Nord Stream - Parte 3
Aplicación de las ecuaciones Básicas y AGA para aproximar el flujo máximo en un gasoducto de larga distancia
Por
Jay Rajani, Ph.D., Kindra Snow-McGregor, P.E., Mahmood Moshfeghian, Ph.D
Introducción
En seguimiento de los dos últimos Previos del Mes (TOTM/PDM) sobre el gasoducto Nord Stream de larga distancia, el cual transmite el gas natural desde Rusia hasta Europa, este PDM resume la aplicación de varias correlaciones/ecuaciones disponibles para determinar la capacidad máxima de susodicha línea de larga distancia. Adicionalmente, se pueden realizar cómputos para efectuar cómputos a presión P, lpc/kPa, y temperatura T ºF/ºC ; demostrando que un gasoducto de larga distancia puede ser aplicado también para estimar como estas líneas igualmente pueden ser aplicadas para proporcionar volumen de almacenamiento del gas.
Data para el Caso en Estudio:
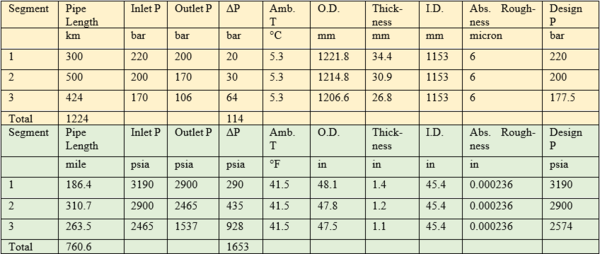
En los previos PDM hemos discutido los varios parámetros que están disponibles en el dominio público [3] y presentados en la Tabla 1. Nord Stream 1 posee dos (2) líneas paralelas, y cada una de ellas posee la capacidad para transportar en gas desde Rusia hasta Alemania a un caudal de 75.34 millones de PCSestd m3/día (2660.6 MMPCSD).
Tabla 1. Especificaciones del Gasoducto en unidades SI y FPS
Como la composición del gas transportado en los gasoductos NSI no ha sido publicado, fue asumido en este estudio que la composición del gas Noruego presentado en la Tabla 2 , transmitido hacia la Placa Continental sería una buena aproximación del gas en el gasoducto NSI.
Tabla 2. Composición del gas de alimentación.
Basado en la data presentada en el cuadro superior, los valores de las propiedades de flujo fueron calculados y presentados en la Tabla 3 respectivamente.
Tabla 3. Resultados calculados para un caudal de gas de 75.34 millones Std m3/dia
Tabla 4. Resultados calculados para un caudal de gas de 2660.6 MMPCE/dia
En este estudio, dos ecuaciones estándar derivadas de la ecuación básica de flujo considerando las condiciones ponderadas han sido aplicadas para estimar la capacidad de la línea NSI. Estas fórmulas son las ecuaciones Básica y AGA (American Gas Association), las cuales incorporan un factor de fricción “f”. Estas relaciones se presentan en [4].
La ecuación AGA estima el factor de fricción bajo dos premisas, “parcialmente turbulento”, y turbulencia completa. La turbulencia parcial es presentada en la ecuación Colebrook-White para las tuberías lisas. La presunción “tubería lisa” es corregida aplicando un factor de arrastre, Ff, el cual reconoce varias condiciones de la tubería: condiciones de la superficie interna, soldaduras, cambios de dirección de flujo, válvulas de aislamiento, etc. La región de “turbulencia completa” existe independiente del número Reynolds, y solo depende de la rugosidad de la línea.
Estas ecuaciones se ven disponibles en el “software” GCAP [5] y la presentación de pantalla de los resultados GCAP se presentan en las Figuras A1 – A5 en el Apéndice A.
Tabla 5. Resultados calculados para un gas con caudal de 75.34 millón Est m3/dia
Tabla 6. Resultados Calculados para un Caudal de 2660.6 MMPCSD
La ecuación BASICA aproximo el gasto en 84.07 millones Std m3 (2969 MMscfd) basados en un 100 % de eficiencia. La ecuación BASICA también aproximo un gasto de 75.63 millones Std m3 (2671 MMscfd) considerando un 90 % de eficiencia.
La capacidad publicada de este gasoducto es de 75.34 millones Est m3 de gas [3].
Revisión del caudal igualmente fue aproximado iniciando PROMAX [6], el cual aplica las regiones de fase – única, más la ecuación aplicando el factor de fricción Colebrook. Esta metodología resulto en un gasto de 83.1 millones de m3 (2,934 MMPCSD) de gas.
Las diferencia entre el pronosticado y actual son de 0.4% para 90% básico y 11.6 % para un básico de 100%, 12.3 por AGA y 10.3 % con PROMAX. Considerando que la composición del gas es desconocida para el NSI, estas diferencias se ven razonables.
Espesor de la Chapa
El Gasoducto NS1 pipeline varia en presión operativa, de manera que varia el espesaor de la misma. Aplicando la fórmula de Barlow, se estimó este espesor. La fórmula de Barlow establece la presión interna capaz de mantener la línea en función de sus dimensiones y resistencia del material férrico
Where: Donde
t = pipe wall thickness, mm (in) - espesor de la tuberia , mm (pul)
P = pressure (taken as) 1.1 x design pressure , MPag (psig) – presion tomada como
1.1 por la presión de diseño. Mpa
S = allowable stress, 483 MPag (70,000 psi) for grade x70 steel – tension permitida.
considerada para 483 MPag (70,000 psi) para el hierro grado x 70, grade x70
D = outside diameter, mm (in) – Diametro Externo, mm (pul)
En la ecuación Barlow, no incorpora una previsión para la corrosión. Si incluimos 3 mm como representativo (cp), se ve lo siguiente:
Aplicando la relación de Barlow, se ha calculado este espesor para distintos segmentos de la línea, y presentado en la Tabla 7.
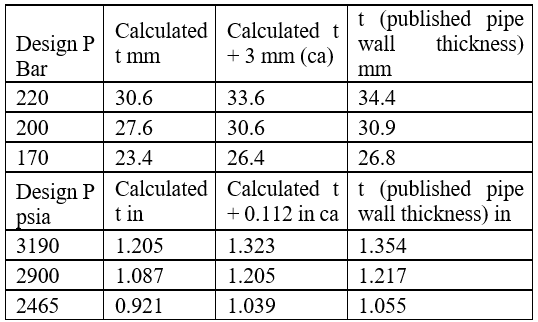
Tabla 7. Espesor de la línea para distintos segmentos
La Tabla 7 expone los espesores del gasoducto (t) con requerimientos de corrosión. Esta Informaron revela buena coincidencia con la data publicada se logra empleando la formula
Empaque de la línea
La tubería NSI igual puede ser aplicada para estimar los requerimientos de almacenamiento de gas, cuando este no se aplica para transporte. La metodología aplicada para estimar el volumen en metros cúbicos de gas (PC).
Este inventario (V) se puede calcular por Inventario (V) de la línea se puede calcular mmediante:
Asumiendo un diámetro interno del gasoducto en 1.153 m (3.68 pie) y longitud de 1 224 000 m (4 015 748 ft), El volumen seria 1 277 997 m3 (12 578 711 ft3 / pie3).
Aplicando la ley del gas natural tenemos:
PV = nZRT
o volumen molar:
Donde P es la presion ponderada entre entrada (22000 kPa or 3190 lpca) y descarga (10600 kPa or 1537 lpca), estas presiones reflejan 16300 kPa (23663 psia), T es la temperatura ponderada en el gasoducto (5 ⁰C=41°F o 278 K=500.4 °R), Z es la compresibilidad de of 0.75 and R es la constante universal del gas (8.314 kPa.m3/kmol. K o 10.732 lpca.pie3/lbmol-°R).
n = 12 017 147 kmol (26 497 809)
Ahora 1 kmol = 23.64 Est. m3 y 1 lbmol = 379.5 pcs
De manera que los metros cúbicos estándar de gas el cual puede ser puesto en el gasoducto 284.1 millones Est. m3 (10.6x109 pcs).
Esta es la cantidad del gas que puede ser almacenada en el gasoducto cundo no opera en fase de transportación.
Comentarios en Conclusión:
La metodología aplicada arriba demuestra como los gasoductos de larga distancia con correlaciones/líneas de gas, aplicando (ecuaciones BASIC and AGA ) pueden ser aplicadas en la evaluación de los gastos de diseño . Se notó que la Ecuación Básica con 90 % de eficiencia reflejo los resultados medidos en capacidades muy cercana con ecuación básica con eficiencia de 90 %. Fue notado que la ecuación Básica con 90 % reprodujo con mucha cercanía los resultados medidos de las citadas líneas de flujo.
Para la metodología de Barlow en el cómputo de los espesores, igual, expreso buen acuerdo con material publicado.
En adición, aplicando la ley de gas natural, se puede demostrar que grandes cantidad de gas puede ser línea/empacada, cuando esta no esté en operaciones.
Para informarse de casos similares y como minimizar problemas operacionales, le sugerimos su asistencia a nuestras sesiones técnicas G4 (Gas Conditioning and Processing), P81 (CO2 Surface Facilities), mas PF4 (Oil Production and Processing Facilities).
por autores:
Jay Rajani, Ph.D., Kindra Snow-McGregor, P.E., Mahmood Moshfeghian, Ph.D.
Traducción en Español: Dr. Frank E. Ashford
References:
1. Moshfeghian, M., Rajani, J., and Snow-McGregor, K., “Transportation of Natural Gas in Dense Phase – Nord Stream”, PetroSkills TIP OF THE MONTH, April 2022.
2. Langer, J.F, Snow-McGregor, K, and Rajani, J., “Part 2: Nord Stream Pipelines – Multiple Parallel Paths to Success or Failure?”, PetroSkills TIP OF THE MONTH, April 2022.
3. Beaubouef, B., “Nord stream completes the world’s longest subsea pipeline,” Offshore, P30, December 2011.
4. Campbell, J.M., “Gas Conditioning and Processing, Volume 1: The Fundamentals,” 9th Edition, 3rd Printing, Editors Hubbard, R., and Snow–McGregor, K., Campbell Petroleum Series, Norman, Oklahoma, PetroSkills 2018
5. 5.GCAP 10.2.1, Gas Conditioning and Processing, PetroSkills/Campbell, Tulsa, Oklahoma, 2022.